Selection of appropriate operation parameters for orbital mixing using a mathematical model illustrated at the example of a 384-well microplate
Authored by: Alexander Schenk zu Schweinsberg, Olaf Simmat, Daniel Toro, Andreas Vester
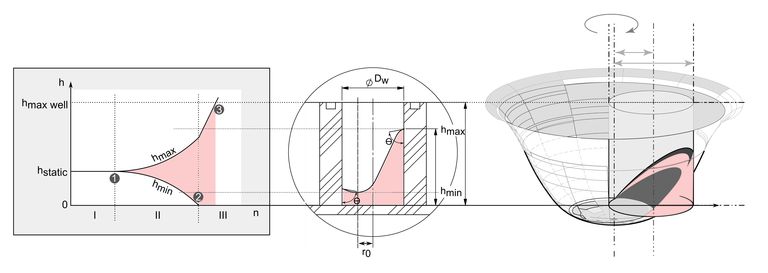
The article presents a general framework, that is based on the current status of an inhouse developed simulation model, for the efficient calculation of liquid distribution, with the aim to optimize mixing conditions in small microplate wells commonly used in laboratory automation processes.
Generally known and established methods that are valid for larger laboratory vessels, frequently used in several biotechnology applications, consider the viscosity of the liquid as the significant factor for the process. The presented model stands out from present simulation methods as it takes the surface tension, as the key factor for liquid distribution in microplate vessels with small diameter into account. The practically applicable and continuously refined mathematical model of the simulation is based on the principles of conversation of energy and minimization of liquid surfaces. The developed differential equations are solved numerically in a semi inverse manner and leads to sufficient results significantly faster then more complex methods.
For that reason, a wide range of parameters can be examined in a reasonable amount of time. With this framework a time efficient way for planning and optimizing applications based on microplate mixing processes is made available. The poster discusses and illustrates the calculation results under consideration of different physical mixing parameters and operation conditions using a 384 well microplate as an example. Experimental measurements with orbital shakers of the BioShake® series were used to validate the generated data.