Authored by: Alexander Schenk zu Schweinsberg, Olaf Simmat, Daniel Toro, Andreas Vester
Selection of appropriate operation parameters for orbital mixing using a mathematical model illustrated at the example of a 384-well microplate
1. Overview
The article presents a general framework, that is based on the current status of an inhouse developed simulation model, for the efficient calculation of liquid distribution, with the aim to optimize mixing conditions in small microplate wells commonly used in laboratory automation processes.
Generally known and established methods that are valid for larger laboratory vessels, frequently used in several biotechnology applications, consider the viscosity of the liquid as the significant factor for the process. The presented model stands out from present simulation methods as it takes the surface tension, as the key factor for liquid distribution in microplate vessels with small diameter into account. The practically applicable and continuously refined mathematical model of the simulation is based on the principles of conversation of energy and minimization of liquid surfaces. The developed differential equations are solved numerically in a semi inverse manner and leads to sufficient results significantly faster then more complex methods.
For that reason, a wide range of parameters can be examined in a reasonable amount of time. With this framework a time efficient way for planning and optimizing applications based on microplate mixing processes is made available. The poster discusses and illustrates the calculation results under consideration of different physical mixing parameters and operation conditions using a 384 well microplate as an example. Experimental measurements with orbital shakers of the BioShake® series were used to validate the generated data.
2. Introduction
The free surface of a liquid sample in a microplate well, under orbital shaking conditions, is taking a parabolic shape if viscosity, surface and interfacial tensions are neglected.
Available literature is presenting an analytical solution method for calculation liquid distribution in conical flasks and other large bioreactor systems without consideration of the surface tension as viscosity is the predominant factor within the examined dimensions [1,2]. Furthermore several methods of Computational Fluid Dynamics (CFD) like the Volume of Fluid (VOF) method are well established for calculation of sloshing problems [4,5]. Because of the complex preprocessing that is necessary these methods are not applicable for users without this specialized knowledge.
Based on the insight, that the surface tension is the key factor to determine the surface shape of the liquid in microplates and similar small scale vessels, we modified the governing equations presented by Lubarda [3] for calculating liquid distribution in a uniformly rotating cylinder in the presence of surface tension in a way so that they are now applicable to the problem of liquid distribution in orbitally shaken microplate wells. The modified equations consider three possible cases of liquid distribution which are illustrated in figure 4. In figure 1 the impact of this modification is shown. The figure displays the differences in the liquid distribution, when calculated with and without consideration of surface tension, in a 384 microplate well. The simulation results are validated against experimental data. It becomes obvious that already at low mixing frequencies the deviation of the maximum resulting liquid height is significant and the results of the experimental data is in correlation with the presented simulation.
The aim of the presented work is to develop a software that allows an end-user the examination and selection of appropriate and reliable technical parameters by entering a few known input values.
3. Methods
In figure 2 the fundamental input parameters for the numerical calculation and commonly scale of values are illustrated. Furthermore in figure 3 the schematic flow diagram of the developed algorithm for the solution of the boundary value problem is shown. The initially constant input parameters entered by the user are modified during the calculation because of the interaction of some physical parameters.
For example the liquid surface tension is temperature sensitive and is adapted due to the given ambient temperature. This is especially important because the surface tension, the wetting properties and the contact line dynamics are important to determine sufficient results.
The values of surface and interfacial tension are the predominant factors for the generation of a macroscopic flow, what is the precondition for small scale mixing processes.
The contact angle q is considered to be the essential factor for the satisfaction of the boundary conditions of the numerical calculation. As long as the liquid is at rest a constant contact angle q can be observed due to the interacting forces at the ideally circular shaped three phase contact line. When the liquid starts to rotate along the wall of the well with the angular velocity of ω, the interfacial contact line changes from the circular shape to an approximately elliptic geometry.
Dynamic wetting on solid surfaces is characterized by a moving contact line. Dynamic wetting results in a dynamic contact angle θ(v), which changes its value with the velocity [5]. The dynamic contact angle θ(v) can be modeled as a function of the dynamic velocity v and the static contact angle θ [9]. Furthermore the dynamic contact angle θ(v) correlates to the capillary number Ca, that is defined as the ratio of viscous forces to interfacial forces Ca=vη/σL.
For the simulation we empirically determined a database of correlations between the dynamic contact angle θ(v) according to the microplate construction materials, liquid sample properties and relative velocities of the interfacial contact line.
Selection of appropriate operation parameters
In most cases the mixing quality rises with the amount of liquid in motion in the well. Hence the aim for a defined amount of sample is to select the appropriate frequency at the given orbital radius of the instrument that leads to a maximum amount of liquid in motion in the well without spilling.
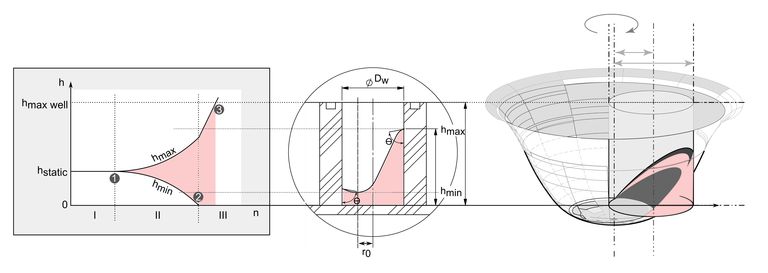
In figure 5 the liquid distribution in a microplate well under orbital acceleration is illustrated schematically. Up to a value of nmin no relevant increase of liquid height in relation to the initial liquid height hstatic can be observed. The value of nmin can be calculated according to the equation shown in figure 5 [7]. If the threshold shaking frequency nmin is exceeded the liquid surface starts increasing due to the centrifugal force overcoming the surface tension. With increasing mixing frequency n the liquid starts rotating along the wall of the microplate well and the liquid height hmin decreases towards the bottom while hmax moves in the top direction.
To select appropriate instrument parameters for the mixing process a maximum value of hmax - hmin can be used. This height difference is an indicator for the development of the macroscopic liquid flow and therefore a good parameter for efficient mixing conditions. If no spilling occurs a mixing frequency at which hmin touches the bottom should be strived.
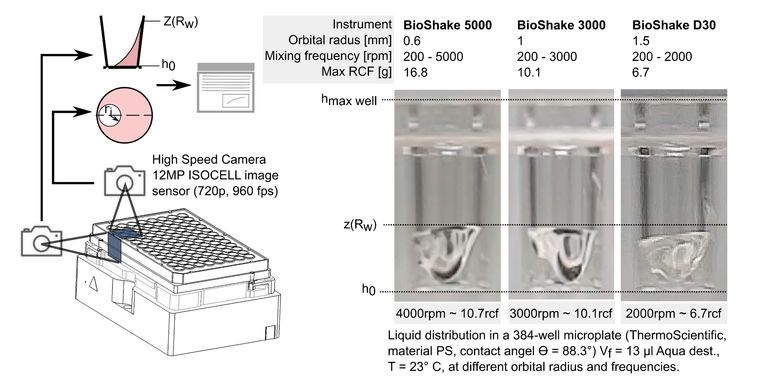
Experimental data for validation of calculated results were generated with orbital shakers of the BioShake® series. The experimental setup and relevant specifications of the instruments are shown in figure 4. The liquid motion in the 384 well microplate under orbital shaking conditions was observed from the side to determine the liquid height and from above to identify the mixing frequency at which the bottom of the vessel is free from liquid.
4. Results
In figure 5, exemplary the numerical calculated minimum and maximum liquid heights are presented for different mixing amplitudes and orbital radius for a filling volume of VF=13µl. In figure 4, corresponding experimental results at 2000, 3000 and 4000 rpm are shown.
It can be observed that the shakers with 0.6 and 1 mm orbital radius are showing a slightly better mixing performance than the Shaker with 1.5 mm . Both of them are able to generate a sufficiently high centrifugal acceleration to decreases hmin to the vessel bottom. For this relatively small volume all three Shakers might be a suitable choice, but with an increase of volume only the 0.6 mm Shaker has the resources to further increase the frequency to maximize ∆∆h.
In figure 6 two calculations for the maximum liquid height at a defined mixing frequency and corresponding experimental results with the same 384 well microplate, with an increased filling volume of VF=26µl, are shown. The calculations differ in the value for the contact angle and the difference between the curves illustrates the impact of using a constant contact angle (θ=88.3°) versus using the dynamic contact angle. The experimental data shows a significantly better agreement with the simulation based on the dynamic contact angle.
5. Conclusion
The selection of appropriate operation parameters for orbital mixing is commonly based on time and cost-intensive empirical experiments. It is likely that wrong decisions are influencing the results and cause additional costs and problems especially if cross contamination through randomly occurring spilling. In contact with our customers we observe that in some applications despite the use of suited mixing instruments no efficient liquid motion within 384 well microplates is generated due to the selected operation conditions. For that reason a reliable prediction of liquid distribution in small microplate wells under orbital mixing conditions offers a major benefit to save time, money and optimize application results .
The developed and presented algorithm is continuously improved and extended. A database of valid parameters as a function of their interrelation is the foundation of the numerical calculation. The use of a dynamic contact angle θ(v) lead to sufficient accurate simulation result compared to experimental data. This underlines that the contact angle is an essential factor for the satisfaction of the boundary conditions of the differential equations used in the simulation.
References
[1] BÜCHS, J. et. Al.: Calculating liquid distribution in shake flasks on rotary shakers a. In: Biochemical Engineering Journal. 34 (2007), pp.200-208
[2] BÜCHS, J. et. Al.: Time efficient way to calculate Oxygen transfer Areas and power input in cylindrical disposable shaken bioreactors.
In: Biotechnology progress. 30 (2014), No. 6, pp.1441-1456
[3] LUBARDA, V.A. : The shape of a liquid surface in a uniformly rotating cylinder in the presence of surface tension.
In: Acta Mechanica 224 (2013) No.7, pp.1365-1382
[4] DISCACCIATI, M et.Al.: Numerical solution of orbitally shaken vicous fluids with free surface. In: Int J Numer Meth Fluids.
2013, No. 71, pp. 294-315
[5] RECLARI, V.: Hydrodynamics of orbital shaken bioreactors [Ph.D. Thesis], Laboratoire de Machines Hydrauliques,
Ecole Polytechnique Federale de Lusanne, 2013
[6] DOERFLER, W. et. Al.: Fluid Flow with Dynamic Contact Angle: Numerical Simulation. In: ZAMM (82) 2002 3, pp167-176
[7] HERRMANN, R. et AL: Characterisation of Gas-Liquid Mass Transfer Phenomena in Microplates.
In: Biotechnology and Bioengineering 81 (2003), No. 2, pp. 178-186
[8] BÜCHS, J. ET AL.: Out-of-phase operating conditions, a hithero unknown phenomenon in shaking bioreactors.
In: Biochemical Engineering Journal (2001), No. 7, pp. 135-141
[9] van MOURIC, S et. Al.: Simulation of Capillary Flow with a Dynamic Contact Angle. In: Microgravity sci. technol. XVII-3 (2005), pp. 91-98